संख्या प्रणाली

हम हमारे आस पास जो कुछ देखते/सुनते हैं यह एक प्रकार का डाटा है। इसे हम एनालाॅग डाटा के रूप में परिभाषित करते हैं। लेकिन कम्प्यूटर डाटा को इस रूप में स्टोर नहीं कर सकता इसलिए इसे डिजिटल रूप में परिवर्तित किया जाता है। कम्प्यूटर की मेमोरी में इसे 0 और 1 के रूप में स्टोर किया जाता है। जिसे बाइनरी संख्या प्रणाली कहा जाता है।

एनालॉग डेटा का उपयोग अक्सर भौतिक मात्राओं, जैसे ध्वनि तरंगों, प्रकाश तरंगों और विद्युत संकेतों को प्रदर्शित करने के लिए किया जाता है। डिजिटल डेटा का उपयोग अक्सर असतत मात्राओं, जैसे संख्या, अक्षर और प्रतीकों को प्रदर्शित करने के लिए किया जाता है।

Data representation डेटा को एक रूप से दूसरे रूप में परिवर्तित करने की प्रक्रिया है। एनालॉग और डिजिटल डेटा के संदर्भ में, Data representation एनालॉग डेटा को डिजिटल डेटा या इसके विपरीत परिवर्तित करने की प्रक्रिया है।

Data representation के दो मुख्य तरीके हैं:

एनालॉग-टू-डिजिटल रूपांतरण (ADC) एनालॉग डेटा को डिजिटल डेटा में परिवर्तित करता है। यह नियमित अंतराल पर एनालॉग सिग्नल का नमूना लेकर और फिर नमूनों को डिजिटल मूल्यों में परिवर्तित करके किया जाता है।

डिजिटल-से-एनालॉग रूपांतरण (DAC) डिजिटल डेटा को एनालॉग डेटा में परिवर्तित करता है। यह एक एनालॉग सिग्नल उत्पन्न करके किया जाता है जो डिजिटल मूल्यों से मेल खाता है।

डिजिटाइज़र एक हार्डवेयर डिवाइस है जो एनालॉग सूचना जैसे ध्वनि या प्रकाश प्राप्त करता है और इसे डिजिटल रूप में परिवर्तित करता है।

नंबर सिस्टम (संख्या प्रणाली)

एक संख्या प्रणाली संख्याओं को प्रदर्शित करने का एक तरीका है। सबसे आम संख्या प्रणाली दशमलव संख्या प्रणाली है, जो संख्याओं को प्रदर्शित करने के लिए अंक 0-9 का उपयोग करती है। अन्य लोकप्रिय संख्या प्रणालियों में बाइनरी, ऑक्टल और हेक्साडेसिमल शामिल हैं।

एक कंप्यूटर में, बहुधा उपयोग की जाने वाली संख्या प्रणाली बाइनरी होती है। बाइनरी एक बेस-2 संख्या प्रणाली है, जिसका अर्थ है कि यह केवल दो अंकों का उपयोग करती है: 0 और 1। बाइनरी नंबर में प्रत्येक अंक 2 की शक्ति को प्रदर्शित करता है। उदाहरण के लिए, बाइनरी नंबर 10101 दशमलव संख्या 13 का प्रतिनिधित्व करता है, क्योंकि 1 * 2⁴ + 0 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2^⁰ = 13।

कंप्यूटर में बाइनरी नंबर का उपयोग किया जाता है क्योंकि इलेक्ट्रॉनिक स्विच का उपयोग करके उनको प्रदर्शित करना आसान होता है। एक स्विच या तो चालू या बंद हो सकता है, जो बाइनरी अंक 1 और 0 से मेल खाता है। यह डिजिटल सर्किट का उपयोग करके डेटा को इलेक्ट्रॉनिक रूप से संग्रहीत और हेरफेर करना संभव बनाता है। आमतौर पर इस्तेमाल की जाने वाली संख्या प्रणाली में बाइनरी (बेस-2), ऑक्टल (बेस-8), डेसीमल (बेस-10) और हेक्साडेसिमल (बेस-16) शामिल हैं।

संख्या प्रणाली के प्रकार

बाइनरी संख्या प्रणाली (Binary Number System) : इसमें मात्र दो अंको (0 तथा 1) से ही सारी संख्या निरूपित की जाती है। बाइनरी संख्या प्रणाली का आधार 2 है। यह कंप्यूटिंग और डिजिटल सिस्टम में व्यापक रूप से उपयोग किया जाता है।

उदाहरण : (1111000)₂

ऑक्टल संख्या प्रणाली (Octal Number System) : इसमें आठ अंको (0, 1, 2, 3, 4, 5, 6, 7) का उपयोग किया जाता है। ऑक्टल संख्या प्रणाली का आधार 8 होता है। यह आमतौर पर कंप्यूटर प्रोग्रामिंग में उपयोग किया जाता है, विशेष रूप से बिट्स के समूहों का प्रतिनिधित्व और हेरफेर करने के लिए।

उदाहरण : (170)₈

डेसिमल संख्या प्रणाली (Decimal Number System) : इसमें 10 अंको (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) का उपयोग किया जाता है। डेसिमल संख्या प्रणाली का आधार 10 होता है। दशमलव प्रणाली रोजमर्रा की जिंदगी में इस्तेमाल होने वाली संख्या प्रणाली है।

उदाहरण : (129)₁₀

हैक्सा डेसिमल संख्या प्रणाली (Hexa Decimal Number System) : इस प्रणाली का आधार 16 है अर्थात 16 संकेत या अंक प्रयुक्त किये जा सकते है ये है 0,1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E तथा F अर्थात् यहां कुल 10 अंक (0 से 9) दशमलव (डेसिमल ) प्रणाली से है और संकेत A से F अंग्रेजी वर्णमाला से है। जहां A 10 को दर्शाता है, B 11 को दर्शाता है,......, F 15 को दर्शाता है। इसे बेस 16 सिस्टम या केवल हेक्स के रूप में भी जाना जाता है। इसका उपयोग अक्सर कंप्यूटिंग में बाइनरी नंबरों को अधिक संक्षिप्त रूप से दर्शाने के लिए किया जाता है। प्रोग्रामिंग और डिजिटल सिस्टम में हेक्साडेसिमल संख्या का व्यापक रूप से उपयोग किया जाता है।

उदाहरण : (F9D)₁₆

Number System Conversion Table

Binary	Octal	Decimal	Hexadecimal
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

संख्या प्रणालियों के बीच रूपांतरण

दशमलव संख्या प्रणाली मनुष्यों द्वारा सबसे अधिक उपयोग की जाती है, लेकिन डिजिटल सिस्टम बाइनरी नंबरों को समझते हैं; जबकि ऑक्टल और हेक्साडेसिमल नंबर सिस्टम का उपयोग हमें समझने के लिए बाइनरी प्रतिनिधित्व को सरल बनाने के लिए किया जाता है।

दशमलव से अन्य संख्या प्रणालियों में रूपांतरण

दशमलव संख्या को किसी अन्य संख्या प्रणाली (बाइनरी, ऑक्टल या हेक्साडेसिमल) में बदलने के लिए, नीचे दिए गए चरणों का उपयोग करें।

चरण 1: दी गई संख्या को संख्या प्रणाली के आधार मान (बेस) से विभाजित करें जिसमें इसे परिवर्तित किया जाना है

चरण 2: शेष को नोट करें

चरण 3: भागफल को आधार मान से विभाजित करते रहें और शेष को तब तक नोट करें जब तक कि भागफल शून्य न हो जाए

चरण 4: नोट किए गए शेषों को उल्टे क्रम में लिखें (नीचे से उपर तक)

दशमलव से बाइनरी परिवर्तन (Decimal To Binary Conversion) : दशमलव से बाइनरी परिवर्तन में दिए गए दशमलव अंक को 2 से भाग दे, जब तक सम्भव हो और शेष को उल्टे क्रम में लिखने से बाइनरी संख्या प्राप्त होती है।

उदाहरण : (57)₁₀ = ( ? )₂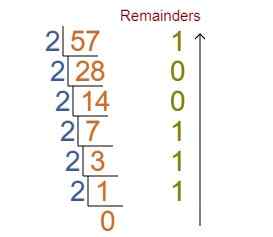

परिणाम : (57)₁₀ = (111001)₂

दशमलव से ऑक्टल परिवर्तन (Decimal to Octal) : दशमलव से ऑक्टल परिवर्तन में दिए गए दशमलव अंक को 8 से भाग दे और शेष को उल्टे क्रम में लिखने से ऑक्टल संख्या प्राप्त होती है।

उदाहरण : (148)₁₀ = (?)₈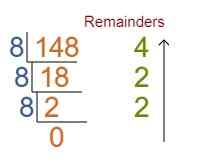

परिणाम : (148)₁₀ = (224)₈

दशमलव से हैक्सा दशमलव परिवर्तन (Decimal to Hexadecimal Conversion) : दशमलव से हैक्सा दशमलव परिवर्तन के लिए दिए गए दशमलव अंको को 16 से भाग दें जब तक सम्भव हो और शेष को उल्टे क्रम में लिखने से हैक्सा संख्या प्राप्त होगी।

उदाहरण : (523)₁₀ = (?)₁₆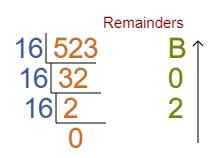

परिणाम : (523)₁₀ = (20B)₈ शेष 11 = B है।

अन्य संख्या प्रणालियों से दशमलव संख्या प्रणाली में रूपांतरण

हम निम्नलिखित चरणों का उपयोग आधार मान (बेस) के साथ दी गई संख्या को उसके दशमलव समतुल्य में बदलने के लिए कर सकते हैं, जहाँ आधार मान क्रमशः बाइनरी, ऑक्टल और हेक्साडेसिमल संख्या प्रणाली के लिए 2, 8 और 16 हो सकता है।

चरण 1: दी गई संख्या में प्रत्येक अक्षरांकीय के लिए स्थिति संख्या लिखें

चरण 2: इस स्थिति संख्या को आधार मान के घात के रूप में लिखें और स्थितीय मान मान प्राप्त करें

चरण 3: दशमलव मान प्राप्त करने के लिए प्रत्येक अंक को संबंधित स्थितीय मान से गुणा करें

चरण 4: समतुल्य दशमलव संख्या प्राप्त करने के लिए इन सभी दशमलव मानों को जोड़ें

बाइनरी से डेसीमल परिवर्तन (Binary to Decimal Conversion) : बाइनरी से दशमलव परिवर्तन के लिए दिए गए है बाइनरी संख्याओं की स्थिति को 2 की घात बनाकर उसे प्रत्येक बाइनरी संख्या से गुणा करते है तथा अन्त में सभी जोड देते है।

उदाहरण : (10011011)₂ = (?)₁₀

परिणाम : (10011011)₂ = (155)₁₀

ऑक्टल से डेसीमल परिवर्तन (Octal to Decimal Conversion) : ऑक्टल संख्या को डेसीमल में परिवव्रित करने के लिए सभी ऑक्टल संख्या की स्थिति को 8 की घात बनाकर उसे गुणा करते है अन्त में सभी गुणनफलो को जोड़ देते है।

उदाहरण : (42)₈ = (?)₁₀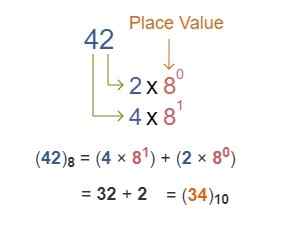

परिणाम : (42)₈ = (34)₁₀

हैक्साडेसीमल से डेसीमल परिवर्तन (Hexadecimal to Decimal conversion) : हैक्सा डैसीमल संख्या से डेसीमल (दशमलव) संख्या में परिवर्तन करने के लिए सभी हैक्सा संख्या तथा वर्णमाला के समतुल्य संख्या लिखते है और सभी हैक्सा संख्या की स्थिति को 16 की घात बनाकर उसे गुणा करते है अन्त में सभी गुणनफलो को जोड़ देते है।

उदाहरण : (B3DE)₁₆ = (?)₁₀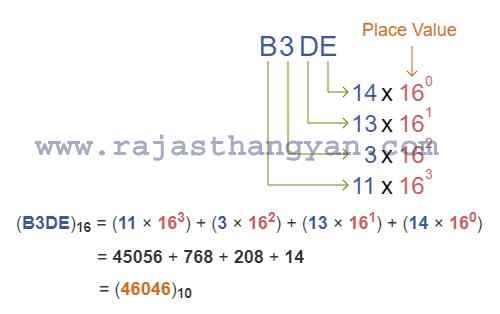

परिणाम : (B3DE)₁₆ = (46046)₁₀

बाइनरी नंबर से ऑक्टल/ हेक्साडेसिमल संख्या में रूपांतरण और इसके विपरीत

एक बाइनरी नंबर को क्रमशः 3 और 4 बिट्स के समूह बनाकर और प्रत्येक समूह को उसके समतुल्य ऑक्टल/हेक्साडेसिमल अंक द्वारा प्रतिस्थापित करके ऑक्टल या हेक्साडेसिमल संख्या में परिवर्तित किया जाता है।

बाइनरी से ऑक्टल परिवर्तन (Binary to Octal Conversion) : बाइनरी संख्या को ऑक्टल संख्या में परिवर्तन करने के लिए दिए गए बाइनरी संख्या में तीन अंको का समूह बनाकर, फिर प्रत्येक समूह की आक्टल संख्या का पता लगाए। आवश्यकता पड़ने पर सबसे बाई ओर तीन बिट का समूह पूरा करने के लिए शुन्य अंक बढ़ाए जा सकते हैं।

उदाहरण : (111110011001)₂ = (?)₈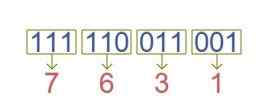

परिणाम : (111110011001)₂ = (7631)₈

ऑक्टल से बाइनरी परिवर्तन (Octal to Binary Conversion) : ऑक्टल संख्या का बाइनरी संख्या में परिवर्तन करने के दिए गए ऑक्टल संख्या को बाइनरी संख्या के तीन तीन Bits के समूह में लिखते है।

उदाहरण- (531)₈ = (?)₂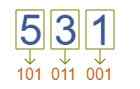

परिणाम : (531)₈ = (101011001)₂

बाइनरी से ईक्साडेसीमल परिवर्तन (Binary to Hexadecimal Conversion) : बाइनरी संख्या को हल्लाडेसीमल संख्या में परिवर्तन करने के लिए दिए गए बाइनरी संख्या के चार अंको का समूह बनाकर और फिर प्रत्येक समूह की हैक्साडेसीमल संख्या का पता लगाए।

उदाहरण : (111110011001)₂ = (?)₁₆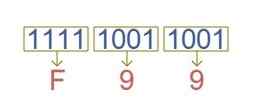

परिणाम : (111110011001)₂ = (F99)₁₆

हैक्सा डैसीमल से बाइनरी परिवर्तन (Hexadecimal to Binary Conversion) : हैक्सा डैसीमल संख्या से बाइनरी में परिवर्तन करने के लिए सभी हैक्सा संख्याओं का चार चार bits का समूह बनाते हुए लिखते है।

उदाहरण : (9DBA5)₁₆ = (?)₂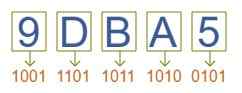

परिणाम : (9DBA5)₁₆ = (10011101101110100101)₂

नोट : हैक्साडेसीमल संख्या से ऑक्टल संख्या में परिवर्तन के लिए सबसे पहले हैक्साडेसीमल संख्या को बाइनरी संख्या में परिवर्तित करते है और फिर बाइनरी संख्या को ऑक्टल संख्या में परिवर्तित करते है।

भिन्नात्मक भाग के साथ एक संख्या का रूपांतरण

अब तक, हम मोटे तौर पर पूर्ण संख्या के लिए अलग-अलग रूपांतरणों से निपटते थे। इस खंड में, हम भिन्नात्मक भाग के साथ संख्याओं के रूपांतरण के बारे में सीखेंगे।

भिन्नात्मक भाग के साथ दशमलव संख्या अन्य संख्या प्रणाली के लिए

एक दशमलव संख्या के भिन्नात्मक भाग को आधार मान के साथ दूसरी संख्या प्रणाली में बदलने के लिए, भिन्नात्मक भाग को आधार मान से बार-बार गुणा करें जब तक कि भिन्नात्मक भाग 0 न हो जाए। उस संख्या प्रणाली में समतुल्य संख्या प्राप्त करने के लिए ऊपर से नीचे तक पूर्णांक भाग का उपयोग करें। यदि भिन्नात्मक भाग क्रमिक गुणन में 0 नहीं बनता है, तो 10 गुणन के बाद रुकें। कुछ मामलों में, भिन्नात्मक भाग दोहराना शुरू कर सकता है, फिर आगे की गणना बंद कर दें।

उदाहरण : (0.675)₁₀ = (?)₂

चूँकि भिन्नात्मक भाग (.400) परिकलन में दोहराव वाला मान है, इसलिए गुणन रोक दिया जाता है। भिन्नात्मक भाग के लिए बाइनरी संख्या प्राप्त करने के लिए पूर्णांक भाग को ऊपर से नीचे तक लिखें।
परिणाम : (0.675)₁₀ = (0.1010110)₂

इसी प्रकार ऑक्टल के लिए 8, हैक्सा डैसीमल के लिए 16 से गुणा करेंगे।

दशमलव संख्या प्रणाली के भिन्नात्मक भाग के साथ गैर-दशमलव संख्या

आधार मान का उपयोग करके दी गई संख्या में प्रत्येक अंक के स्थितीय मान की गणना करें। भिन्नात्मक भाग के साथ समतुल्य दशमलव संख्या प्राप्त करने के लिए स्थितीय मान और अंक का गुणनफल जोड़ें।

उदाहरण : (100101.101)₂ = (?)₁₀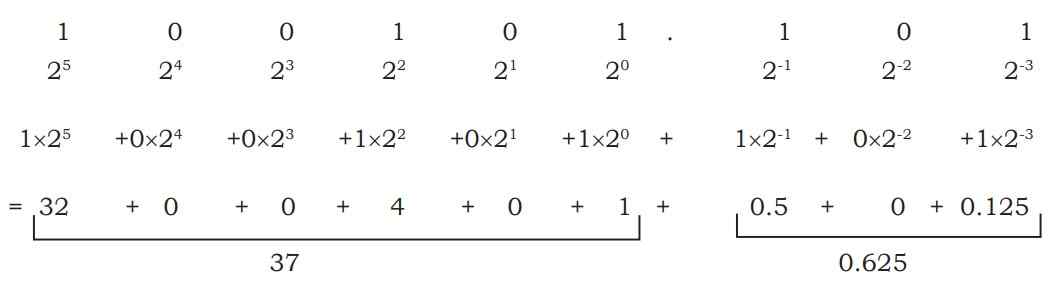

परिणाम : (100101.101)₂ = (37.625)₁₀

इसी प्रकार ऑक्टल के लिए 8 और हैक्सा डैमीमल के लिए 16 की घात से गुणा कर जोड़ेंगे।

ऑक्टल या हेक्साडेसिमल संख्या के लिए भिन्नात्मक बाइनरी संख्या

भिन्नात्मक बाइनरी संख्या को ऑक्टल या हेक्साडेसिमल मान में बदलने के लिए, 3-बिट या 4-बिट के समूह को संबंधित अंक द्वारा पूर्णांक भाग में बदलें। इसी तरह, बाएँ से दाएँ शुरू होने वाले भिन्नात्मक भाग के लिए 3-बिट या 4-बिट के समूह बनाएँ, और प्रत्येक समूह को उसके समकक्ष अंक या ऑक्टल या हेक्साडेसिमल संख्या प्रणाली में प्रतीक द्वारा प्रतिस्थापित करें। 3 या 4 बिट्स का एक आदर्श समूह बनाने के लिए भिन्नात्मक भाग के अंत में 0s जोड़ें।

उदाहरण : (10101100.01011)₂ = (?)₈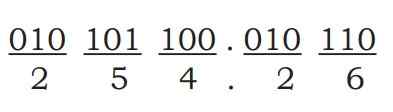

परिणाम : (10101100.01011)₂ = (37.625)₈

इसी प्रकार हेक्साडेसिमल के लिए 4-बिट के समुह बनाने हैं।

कंप्यूटर कोड

कंप्यूटर में, किसी भी वर्ण जैसे अक्षर, अंक या विशेष वर्ण को 1 और 0 के संग्रह द्वारा एक अद्वितीय कोडित पैटर्न में दर्शाया जाता है।

कंप्यूटर में, कोड बाइनरी पोजीशन के निश्चित आकार के समूहों से बना होता है। आमतौर पर उपयोग की जाने वाली बाइनरी कोडिंग योजनाएँ इस प्रकार हैं -

बाइनरी कोडेड डेसीमल (बीसीडी)

यह प्रणाली आईबीएम द्वारा विकसित की गई थी। यह एक संख्या प्रणाली है जहां प्रत्येक दशमलव अंक का प्रतिनिधित्व करने के लिए चार बिट्स का उपयोग किया जाता है। बीसीडी दशमलव अंकों (0-9) का प्रतिनिधित्व करने के लिए द्विआधारी अंकों का उपयोग करने की एक विधि है। बीसीडी प्रणाली में किसी संख्या के आकार की कोई सीमा नहीं होती है।

अमेरिकन स्टैंडर्ड कोड फॉर इंफॉर्मेशन इंटरचेंज (ASCII)

ये मानक वर्ण कोड हैं जिनका उपयोग डेटा को संग्रहीत करने के लिए किया जाता है ताकि इसका उपयोग अन्य सॉफ़्टवेयर प्रोग्रामों द्वारा किया जा सके।

मूल रूप से, ASCII कोड दो प्रकार के होते हैं, जो इस प्रकार हैं -

(i) ASCII-7 यह 7-बिट मानक ASCII कोड है। यह 2⁷ = 128 (0 से 127 तक) अद्वितीय प्रतीकों या वर्णों की अनुमति देता है।

(ii) ASCII-8 यह ASCII-7 का विस्तारित संस्करण है। यह एक 8-बिट कोड है, जो 2⁸ = 256 (0 से 255) अद्वितीय प्रतीकों या वर्णों की अनुमति देता है।

एक्सटेंडेड बाइनरी कोडेड डेसीमल इंटरचेंज कोड (EBCDIC)

EBCDIC में, वर्णों को आठ बिट्स द्वारा दर्शाया जाता है। ये कोड उन सूचनाओं को संग्रहीत करते हैं जो अन्य कंप्यूटरों द्वारा पठनीय होती हैं। यह बिट्स के 2⁸ = 256 संयोजन की अनुमति देता है।

UNICODE : UNICODE डेटा में प्रतीक का प्रतिनिधित्व करने के लिए 16-बिट्स का उपयोग करता है। यह चीनी, जापानी जैसी किसी भी भाषा में किसी भी गैर-अंग्रेजी वर्ण, वैज्ञानिक प्रतीक का प्रतिनिधित्व करता है।

लॉजिक गेट

बूलियन आपरेटर अपने कार्यों के लिए बाइनरी संख्या प्रणाली का उपयोग करते है। बाइनरी संख्या प्रणाली केवल दो संख्याओं का प्रयोग करती है। 0 तथा 1 बाइनरी सूचनाओं के परिवर्तन के लिए लॉजिक परिपथ का उपयोग किया जाता है। इसे लॉजिक गेट कहते है।

लॉजिक गेट एक डिजिटल सर्किट का एक बुनियादी बिल्डिंग ब्लॉक है जिसमें एक या दो इनपुट और एक आउटपुट होता है। इनपुट और आउटपुट के बीच संबंध एक निश्चित तर्क पर आधारित होता है। इन गेट को इलेक्ट्रॉनिक स्विच जैसे ट्रांजिस्टर, डायोड का उपयोग करके कार्यान्वित किया जाता है। प्रत्येक गेट के लिए इनपुट-आउटपुट बाइनरी वेरिएबल्स के बीच संबंध को एक सत्य तालिका द्वारा सारणीबद्ध रूप में दर्शाया जा सकता है। प्रत्येक गेट में A और B द्वारा निर्दिष्ट एक या दो बाइनरी इनपुट वेरिएबल और Y या X द्वारा नामित एक बाइनरी आउटपुट वेरिएबल है।

AND Gate : AND गेट इस गेट को (.), यानी (A.B) से भी दर्शाया जाता है। यह True तभी रिटर्न करता है जब दोनों कंडीशन या इनपुट True होते हैं अन्यथा यह False रिटर्न करता है।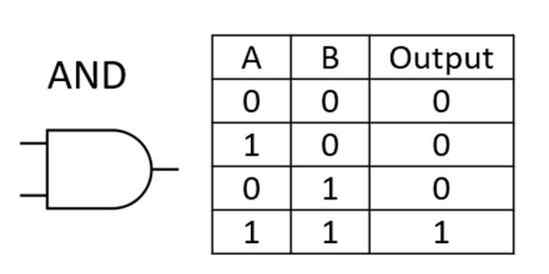

OR Gate : यह गेट दो या दो से अधिक इनपुट का तार्किक योग करता है। इसे (+), यानी (A+B) द्वारा दर्शाया जाता है। यदि कोई एक स्थिति या इनपुट True है तो यह True रिटर्न करता है और यदि दोनों स्थितियाँ False हैं, तो यह False रिटर्न करता है।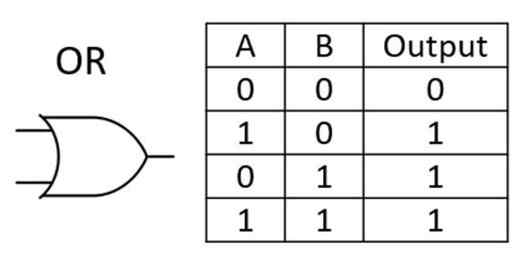

Inverter या NOT Gate : इस गेट को (¯), यानी Ā द्वारा भी दर्शाया गया है। यदि इनपुट False है तो यह True रिटर्न करता है और इसके विपरीत भी है। यानी यदि इनपुट True है तो यह False रिटर्न करता है।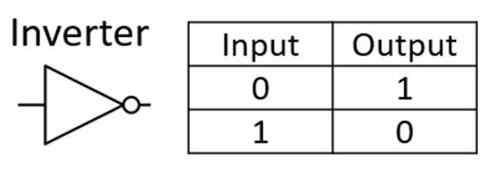

NAND Gate : यह मूल रूप से AND गेट का विलोम है। इस गेट को AND और NOT गेट्स को मिलाकर डिजाइन किया गया है। यह False तभी रिटर्न करता है जब दोनों कंडीशन या इनपुट True होते हैं अन्यथा यह True रिटर्न करता है।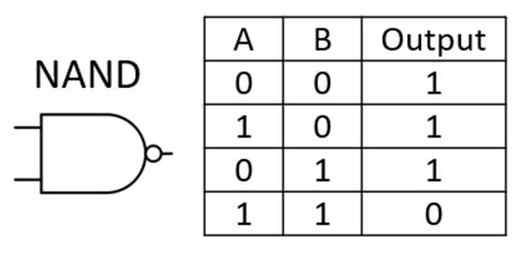

NOR Gate : यह OR गेट का उल्टा होता है। इस गेट को OR और NOT गेट्स को मिलाकर डिजाइन किया गया है। यह केवल तभी True लौटाता है जब दोनों स्थितियाँ या इनपुट False हों अन्यथा यह False रिटर्न करता है।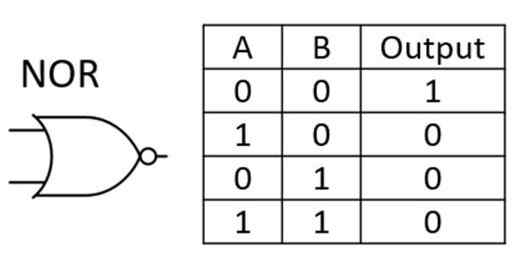

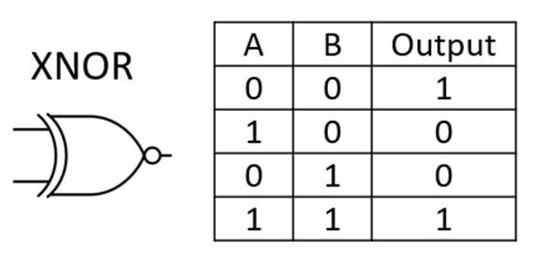
Exclusive-OR या XOR Gate: यह OR गेट के संचालन के आधार पर कार्य करता है। यह केवल तभी True रिटर्न करता है जब दोनों स्थितियों में से एक शर्त True होती है अन्यथा यह False रिटर्न करता है।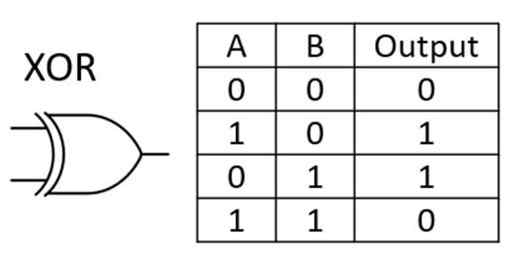

Exclusive NOR या XNOR Gate : यह गेट True तभी देता है, जब दोनों इनपुट समान True, True या False, False होते है।

Start Quiz!