संख्याएं

प्राकृत संख्याएं

जिन संख्याओं का प्रयोग हम प्रकृति या दैनिक जिवन में गिनती के लिए करते हैं। जैसे 1,2,3,4,..... आदि संख्याएं प्राकृत संख्याएं कहलाती हैं। 0 प्राकृत संख्या नहीं है। प्राकृत संख्याओं के समुच्य को "N" से प्रदर्शित किया जाता है।

जैसे N= [1,2,3,...]

उदाहरण के लिए 6 से 12 के बीच प्राकृत संख्याओं का सम्मुच्चय लिखिए -

(7,8,9,10,11)

प्राकृत संख्याओं का वर्गीकरण

1. सम प्राकृत संख्याएं
2. विषम प्राकृत संख्या
3. भाज्य या संयुक्त प्राकृत संख्याएं
4. अभाज्य प्राकृत संख्या
5. न ही अभाज्य न ही संयुक्त

सम प्राकृत संख्या - ऐसी संख्या जिनमें 2 का भाग पुरा-पुरा जाता है सम प्राकृत संख्याएं कहते हैं।

जैसे 2,4,6,8,...... आदि

दो सम संख्या या दो विषम संख्या का योग सदैव एक सम संख्या होता है।

विषम प्राकृत संख्या - ऐसी संख्या जिनमें 2 का भाग पुरा-पुरा नहीं जाता विषम संख्या कहते हैं।

1,3,5,7,........ आदि

एक सम तथा दुसरी विषम संख्या का योग हमेशा विषम संख्या ही होता है।

भाज्य या संयुक्त - ऐसी संख्या जिनमें 1 एवं संख्या के अतिरिक्त किसी अन्य संख्या का भाग पुरा-पुरा जाता है। उन्हें संयुक्त प्राकृत संख्या कहते हैं।

सबसे छोटी संयुक्त प्राकृत संख्या 4 है।

कोई भी संख्या सबसे बड़ी संयुक्त प्राकृत संख्या नहीं है।

अभाज्य प्राकृत संख्या - एक से बड़ी वे संख्या जो 1 या स्वंय को छोड़ कर अन्य किसी भी संख्या से पुर्णतः विभाजित नहीं होती अभाज्य प्राकृत संख्या कहलाती है।

न ही अभ्याज्य न ही भाज्य प्राकृत संख्या - 1 न तो संयुक्त संख्या है और न ही अभाज्य संख्या है।

पुर्ण संख्याएं

प्राकृत संख्या में 0 शामिल कर ले ने से प्राप्त संख्याओं का समुह पुर्ण संख्या कहलाती है। इसे "W" से प्रदर्शित किया जाता है।

जैसे 0,1,2,3,4........ आदि।

पुर्ण संख्या का योग - पुर्ण संख्या का योग सदैव पुर्ण संख्या होता है। अतः पुर्ण संख्याएं योग के लिए संवृत होती है।

जैसे 5+4 = 9

पुर्ण संख्या में योग के दोरान क्रम से कोई फर्क नहीं पड़ता अतः ये क्रम विनिमय है।

6+1=7

1+6=7

पूर्ण संख्या में शुन्य को जोड़ने से उस संख्या में कोई फर्क नहीं पड़ता है। अतः शुन्य पुर्ण संख्याओं के लिए तत्समक अवयव है।

5+0=5

पुर्ण संख्याओं का व्यकलन(घटाव) - पुर्ण संख्याओं का घटाव हमेशा पूर्ण संख्या हो यह आवश्य नहीं है। अतः पुर्ण संख्या व्यकलन के लिए संवृत नहीं है।

पुर्ण संख्याओं का घटाव क्रमविनिमय नहीं होता है। अर्थात

5-4=1

4-5=-1

किसी भी पुर्ण संख्या को उसी पुर्ण संख्या से घटाया जाये तो शुन्य प्राप्त हेाता है।

पुर्ण संख्याओं का गुणा - दो पुर्ण संख्याओं का गुणनफल हमेशा एक पुर्ण संख्या होता है। अतः यह गुणा के लिए संवृत है।

5*4 =20

पुर्ण संख्या के गुणन के दौरान संख्याओं का क्रम बदलने से कोई फर्क नहीं पड़ता। पुर्ण संख्याओं के लिए गुणन क्रमविनिमय होता है।

5*10 =50

10*5 = 50

किसी भी पुर्ण संख्या के लिए 1 गुणन तत्समक है। अर्थात किसी भी पुर्ण संख्या को 1 से गुणा करने पर वही संख्या प्राप्त होती है।

421*1 = 421

पुर्ण संख्याओं का भाग - दो पुर्ण संख्याओं का भागफल आवश्यक नहीं की एक पूर्ण संख्या ही हो अतः पुर्ण संख्याएं भाग के लिए संवृत नहीं है।

19/4= एक पूर्ण संख्या नहीं है।

शुन्य से भाग परिभाषित नहीं है।

भाग के लिए पुर्ण संख्याएं क्रम विनिमेय नहीं है।

किसी भी पुर्ण संख्या को उसी से भाग देने पर सदैव 1 प्राप्त होता है।

पुर्णांक संख्याएं -

पुर्ण संख्याओं में ऋणात्मक संख्याएं शामिल कर दी जाये तो पुर्णांक संख्याओं का निर्माण होता है। इसे "I"या "Z" से प्रकट करते है।

I ={------- -3,-2,-1,0,1,2,3 ------------}

परिमेय संख्याएं

ऐसी संख्याएं जिन्हें p/q के रूप में लिखा जा सकता है। जहां p व q पुर्णांक है। तथा q अशुन्य हैं इनके समुह को Q से प्रकट करते हैं।

जैसे 1/3, 3/1, -6/3 आदि

धनात्म परिमेय संख्या - यदि किसी परिमेय संख्या के अंश और हर दोनों ही धनात्मक अथवा ऋणात्मक हो या दोनो अश और हर के चिन्ह समान हो तो ऐसी संख्याएं धनात्मक परिमेय संख्या कहलाती है।

जैसे 4/5, -5/-4 आदि

ऋणात्मक परिमेय संख्याएं - यदि किसी परिमेय संख्या के हंश एवं हर में से कोई एक ऋणात्मक हो अर्थात अंश एवं हर के चिन्ह विपरित हो तो ऐसी परिमेय संख्याएं ऋणात्मक परिमेय संख्या कहलाती है।

जैसे -5/3, -3/2 आदि

दो संख्याओं के मध्य परिमेय संख्या ज्ञात करना - दि गई संख्याओं के मध्य परिमेय संख्या ज्ञात करने के लिए दोनों संख्याओं को जोड़ कर दो से भाग दिया जाता है।

परिमेय संख्याओं का दशमलव प्रसार

सांत दशमलव प्रसार - जिन संख्याओं का कुछ चरणों के बाद दशमलव प्रसार का अंत हो जाता है।

जैसे 1/2=0.5

3/2=1.5

असांत दशमलव प्र्रसार - जिन संख्याओं का कुछ चरणों के बाद शेष की पुनरावृति होने लगती है। यह प्रसार असांत दशमलव प्रसार कहलाता है।

जैसे 1/3=0.3333........

1/11=.090909......

ऐसी संख्या जिनका हर का अभाज्य गुणनखण्ड xⁿ yⁿ के रूप का नहीं है। जहां n तथा m पुर्णांक है। तो उस संख्या का दशमलव प्रसार असांत आवर्ती होता है।

दशमलव संख्याओं को परिमेय संख्या में बदलना

सांत दशमलव संख्या को परिमेय संख्या में बदलना - सांत दशमलव संख्याओं को परिमेय संख्या में बदलने के लिए दि गई दशमलव संख्या में दशमलव के दांयी और लिखे हुए अंकों को गीन कर हर में 1 के बाद उतने ही शुन्य लगा देंगे।

0.267 = 267/1000

0.24 = 24/100 = 12/50 = 6/25

असांत आवर्ती दशमलव संख्या को परिमेय संख्या में बदलना

असांत आवर्ती दशमलव संख्या को परिमेय संख्या में बदलने के लिए आर्वीत वाले अंकों को अंश में लिखा जाता है। और हर में उतने ही 9 लिखे जाते हैं।

जैसे 0.3333 = 0.3.......= 3/9

यदि किसी दशमलव संख्या में दशमलव के पश्चात एक अथवा अधिक अंकों के बाद अंकों की आवृर्ती होती है। तो ऐसी संख्या को परिमेय संख्या में बदलने के लिए दशमलव व रेखा(आवर्ती वाले अंकों के उपर से) को हटा कर संख्या लिखी जाती है।तथा कुल संख्या में से बिना आवर्ती वाली संख्या घटा दी जाती हैं। तथा शेषफल में आवर्ती वाली संख्या गिनती कर उतने 9 लिखे जाते हैं। तथा बिना आवर्ती वाली संख्या की गिनती कर उतने ही शुन्य 9 के दायीं और लिखे जाते हैं।

0.09 = 09-0/99 =09/99 = 1/11

अपरिमेय संख्याएं

वे संख्याएं जिनको p/q के रूप में नहीं लिखा जा सकता हो वे अपरिमेय संख्या कहलाती है। जैसे

√2, √3, √7आदि

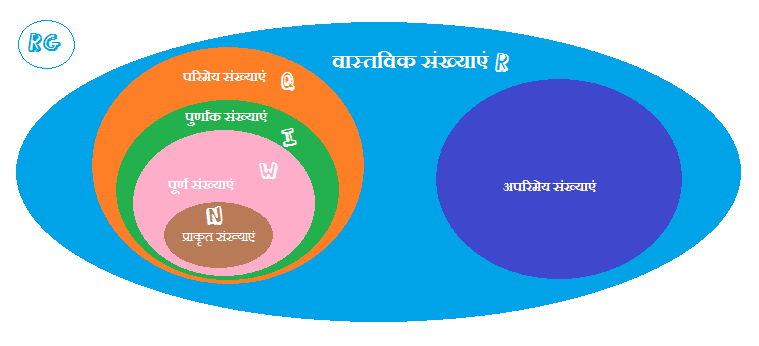
वास्तविक संख्या

परिमेय तथा अपरिमेय संख्याओं को एक साथ लेने पर जो संख्याएं प्राप्त होती है उन्हें वास्तविक संख्या कहते हैं। या वे संख्या जिनका वर्ग करने पर धनात्मक पुर्णांक प्राप्त हो वास्तविक संख्या कहलाती है।

(-4)² = 16, √2, -3 आदि

वास्तविक संख्याओं का दशमलव प्रसार

वास्तविक संख्याओं का सांत दशमलव प्रसार - उदाहरण के लिए हम एक संख्या लेते हैं 1/2 जिसमें 1 को 2 से विभाजित करने पर भागफल 0.5 आता है जिसमें भागफल की पुनरावृति नहीं होती है। ऐसी संख्याओं के दशमलव प्रसार को सांत दशमलव प्रसार कहते हैं।

असांत दशमलव प्रसार - 9/11 = 0.8181..... में भागफल की पुनरावर्ती हो रही है। ऐसी संख्या के दशमलव प्रसार को असांत दशमलव प्रसार कहते हैं।

गणितिय संक्रियाओं का हल करने का क्रम

1. रेखा कोष्ठक
2. कोष्ठक
3. का
4. भाग
5. गुणा
6. जोड़
7. घटाव

इसके लिए Trick - BODMAS

B → Brackets first (parentheses)

O → Of (orders जैसे Powers and Square Roots, Cube Roots, etc.)

DM → Division and Multiplication ( बांए से दांएt)

AS → Addition and Subtraction ( बांए से दांए)

संख्याओं का महत्तम समापवर्तक व लघुत्तम समापवत्र्य

महत्तम समापवर्तक(म.स.)

दो या दो से अधिक संख्यओं का म.स. वह बड़ी से बड़ी संख्या है जो प्रत्येक दी गई संख्या को पुर्णतया विभक्त कर दे।

जैसे 25 तथा 45 का म.स. = 5

लघुत्तम समापवत्र्य (ल.स.)

दि गई संख्याओं का ल.स. वह छोटी से छोटी संख्या है जो दी गई संख्याओं से पुर्ण तया विभाजित हो जाये।

5,20,40 का ल.स. = 40

भिन्नों का ल.स. = अंशों का ल.स./हरों का म.स.

भिन्नों का म.स. = अंशों का म.स./हरों का ल.स.

उदाहरण - 12/7,16/21 का म.स. ज्ञात किजिए -

12 व 16 का म.स. = 2

7 व 21 का ल.स. = 21

अतः 12,16 का म.स./7,21 का ल.स. = 2/21

वर्गमूल व घनमूल

वर्गमूल

किसी संख्या का वर्गमूल वह संख्या है जो अपने से गुणा करने पर दि गई संख्या प्राप्त हो |

जैसे x के वर्गमूल को √x से व्यक्त करते हैं जिसे स्वंय √x से गुणा करने पर x प्राप्त होता है।

जैसे - √4 =2

घनमूल

किसी संख्या का घनमूल वह संख्या है जिसे स्वंय से तीन बार गुणा करने पर वह संख्या प्राप्त होती है जैसे x का घनमूल y है तो y*y*y = x या ³√x=y

जैसे -³√8=2

Start Quiz!