क्षेत्रफल परिमाप
वर्ग
वर्ग एक समतल आकृति है। जिसकी चार भूजाएं होती और चारों भूजाएं समान लम्बाई की होती है तथा चारों कोण समकोण यानी 900 के होते हैं। दो विकर्ण हो जिनकी लम्बाई बराबर होती है।
वर्ग की परिमाप = 4*भूजा (4 भूजाएं जिनकी लम्बाई बराबर)
क्षेत्रफल = (भूजा)2
क्षेत्रफल यदि विकर्ण दिया हो = (विकिर्ण)2/2
विकिर्ण यदि एक भूजा दि हो - भूजा*√2
आयत
आयत भी वर्ग की तरह समतल आकृती है।तथा इसके भी सभी कोण 900 के होते हैं लेकिन चारों भूजाएं समान लम्बाई की नहीं होती बल्की आमने सामने कि भूजाएं समान लम्बाई की होती हैं
आयत का परिमाप = 2*(लम्बाई+चैड़ाई)
क्षेत्रफल = लम्बाई*चैड़ाई
विकिर्ण = √लम्बाई2 +चैड़ाई2
त्रिभूज
त्रिभूज भी एक समतल आकृति है। जिसकी तीन भूजाएं होती है। तथा तिन कोण होते हैं।तीनों कोणों का योग 1800 होता है। त्रिभूज में जो कोण त्रिभूज से बाहर बनता है उसे बहिष्कोण कहते हैं तथा जो कोण त्रिभूज के अन्दर बनता है। उसे अतः कोण कहते हैं बहिष्कोण सामने वाले दोनों अतःकोणों क योग के बराबर होता है।वह त्रिभूज जिसमें एक कोण समकोण यानि 900 का हो तो इसे समकोण त्रिभूज कहते हैं। समकोण के सामने की भूजा कर्ण कहलाती है तथा जिस पर समकोण् होता है उसे आधार कहते हैतथा तिसरी भूजा जो समकोण पर है लम्ब कहलाती है।
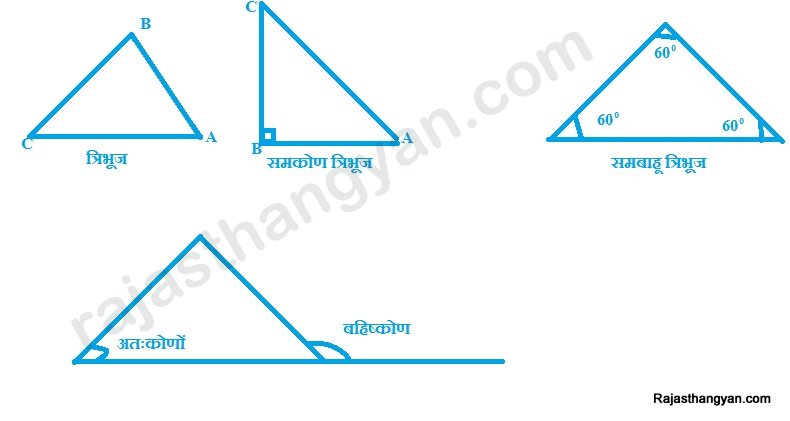
इसका क्षेत्रफल = 1/2*( आ.*उ.) उंचाई = लम्ब
समकोण त्रिभूज की भूजाओं में एक सम्बंध पाया जाता है (pythagoras theorem)
कर्ण2 = आधार2 + लम्ब2
यदि त्रिभूज समकोण त्रिभूज न हो तथा तिनों भूजाए(a,b,c) दि गई हो तो क्षेत्रफल (हिरो का सुत्र ) = √s(s-a)(s-b)(s-c)
यहां s त्रिभुज का अर्ध परिमाप है s = (a+b+c)/2
वह त्रिभूज जिसमें सभी कोण बराबर हो तो इसकी सभी भूजाएं भी बराबर होगी। क्योंकि बराबर कोणों की सम्मूख भूजाएं बराबर होती है। ऐसा त्रिभूज समबाहू त्रिभूज कहलाता है। इसका प्रत्येक कोण 600 का होता है। इस प्रकार के त्रिभूज का क्षेत्रफल = √3/4*(भूजा)2
त्रिभूज की दो भूजाओं का योग तिसरी भूजा से सदैव बड़ा होता है।
चतुर्भूज
एक समतल आकृति है। जिसकी चार भूजाएं होती है तथा चार कोण होते हैं तथा चारों कोणों का योग 3600 होता है। चतुर्भूज कई प्रकार के होते हैं जैसे
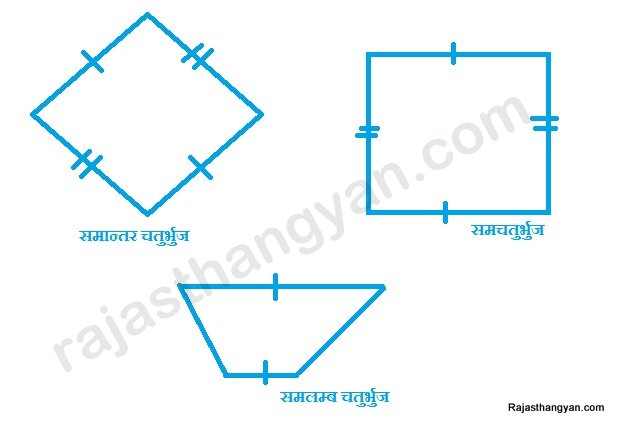समान्तर चतुर्भुज -
ऐसे चतुर्भुज जिसमें आमने सामने की भूजाओं के युग्म समान्तर हो समान्तर चतुर्भूज कहलाते हैं।आयत एक समान्तर चतुर्भुज है लेकिन यह आवश्यक नहीं की प्रत्येक समान्तर चतुर्भुज एक आयत हो। इसका क्षेत्रफल - आधार*उंचाई
यदि किसी समान्तर चतुर्भूज की सभी भुजाएं बराबर हो तो इसे समचतुर्भुज कहते हैं इसका क्षेत्रफल - 1/2 *(विकिर्णों का गुणनफल)
समलम्ब चतुर्भुज
यदि किसी चतुर्भुज में केवल एक युग्म ही समान्तर हो तो इसे समलम्ब चतुभुर्ज कहते हैं।इसका क्षेत्रफल = 1/2*(समान्तर भूजाओं का योग)*(उनके बिच की दुरी)
वृत
वृत्त एक समतल आकृति है जिसके सभी बिन्दु किसी निश्चित बिन्दु से समान दुरी पर स्थित होते हैं निश्चित बिन्दु को वृत्त का केन्द्र कहते हैं।
वृत्त की सबसे छोटी इकाई त्रिज्या मान सकते हैं जो इसके केन्द्र से लेकर इसके किनारे तक कि लम्बाई है। व्यास वृत्त के एक किनारे से लेकर केन्द्र से गुजर कर दुसरे किनारे तक जाने वाली रेखा कि लम्बाई है। यानि व्यास त्रिज्या से दुगना होेता है।
यदि त्रिज्या को r माने तो व्यास 2r होगा।
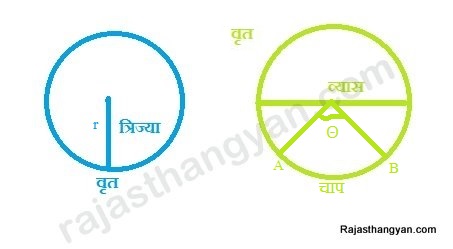
वृत्त की परिधि = 2πr
क्षेत्रफल = πr2
अर्ध वृत्त का क्षेत्रफल = 1/2(πr2)
अर्ध वृत्त की परिधि =πr(2πr का आधा)+ 2r व्यास
चाप की लम्बाई = 2πr(Θ/360) नोट - 2πr कुल परिधि है। जिसमें से 3600 का कोण बनता है। जब कोण Θ बनता है तो वह कुल परिधि का Θ/360 प्रतिशत ही होगा|
चाप का क्षेत्रफल = कुल क्षेत्रफल*(Θ/360) या 1/2(चाप की लम्बाई *त्रिज्या )= 1/2(AB*r)
उदाहरण
एक वर्ग की एक भूजा की लम्बाई 40 सेमी. है इसका क्षेत्रफल होगा -
वर्ग का क्षेत्रफल - भूजा2
-(40)2 - 1600 सेमी2
उदाहरण
एक वर्ग की प्रत्येक भूजा की लम्बाई में 10% वृद्धि करने पर क्षेत्रफल में कितने प्रतिशत की वृद्धि होगी -
माना पहले भूजा थी - 100 मी.
तो क्षे. (100)2 = 10,000 मी.2
10% वृद्धि के बाद भूजा 110 मी. तथा क्षे.= (110)2 = 12,100 मी.2
वृद्धि हुई - 12,100-10,000 - 2100 मी.2
माना 2100 मी.2 10,000 मी.2 का x प्रतिशत है अतः
10,000*x/100 = 2100
x=(2100*100)/10000 = 21%
उदाहरण
एक आयत की लम्बाई 10 सेमी और चैड़ाई 15 सेमी है क्षेत्रफल होगा -
आयत का क्षेत्रफल = लम्बाई*चैड़ाई
= 10*15 = 150 सेमी
उदाहरण
एक आयत की लम्बाई 5 सेमी तथा एक विकिर्ण कि लम्बाई 13 सेमी है आयत का क्षेत्रफल होगा -
हमें आयत की एक भुजा 5 सेमी व विकिर्ण 13 दिया है अतः दुसरी भुजा ज्ञात करनी है इसके लिए हम जानते हैं कि विकिर्ण आयत को दो समकोण त्रिभुजों में बांटता है और समकोण त्रिभुज की भुजाओं में एक सम्बन्ध पाया जाता है।
कर्ण2 = आधार2 + लम्ब2
लम्ब2 = कर्ण2 - आधार2
लम्ब2= 132 - 52
लम्ब2= 169-25 = 144
लम्ब =12
अतः आयत का क्षेत्रफल - 12*5 = 60 सेमी2
उदाहरण
एक बैडमिनटन का कोर्ट जिसकी लम्बाई 30 मी. तथा चैड़ाई 20 मी. है। में लकड़ी के 3*2 मी के टुकड़े लगवाने है। एक टुकड़े का मुल्य 120 रू है तो पुरे कोर्ट में लकड़ी लगवाने में कितना खर्चा होगा -
कोर्ट का क्षेत्रफल = 30*20 = 600 मी.2
टुकड़े का क्षेत्रफल - 3*2 - 6 मी.2
600 मी. में 6 मी. के टुकड़े लगेंगे - 600/6 = 100
एक टुकड़े का मुल्य 120 रू तो 100 टुकड़ों का मुल्य 120*100 = 12,000 रू
उदाहरण
100 मी. लम्बे व 50 मी. चौड़े पार्क में अन्दर की तरफ टहलने के लिए 3 मी. चौड़ी सड़क बनवाने में कितना खर्चा आयेगा यदि खर्चा 50 रू. प्रति वर्ग मी. हो -
पार्क का क्षेत्रफल =100*50 = 5000मी.
पार्क के अन्दर का क्षेत्रफल सड़क को छोड़कर
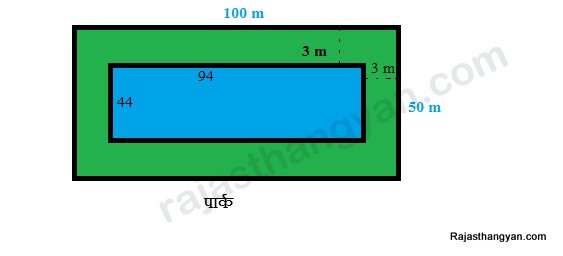
लम्बाई दोनों तरफ 3-3मी. कम हो गई अतः अब लम्बाई = 100-6 = 94 मी.
चैड़ाई भी दोनों तरफ से 3-3मी. कम हो गई अतः अब चैड़ाई = 50-6 = 44 मी.
अतः अन्दर का क्षेत्रफल 94*44 = 4136 मी2
शेष क्षेत्रफल यानी सड़क का क्षेत्रफल = 5000-4136 = 864 मी.2
1 वर्ग मी. का खर्चा 50 रू अतः 864 का खर्चा - 864*50 = 43,200 रू.
उदाहरण
एक समकोण त्रिभुज का आधार 10 सेमी. उंचाई 13 सेमी. है त्रिभुज का क्षेत्रफल -
त्रिभुज का क्षेत्रफल - 1/2(आधार*उंचाई)
= (13*10)/2 =130/2 = 65 सेमी.2
उदाहरण
एक त्रिभुज की तीन भुजाएं 8,10,6 हैं त्रिभुज का क्षेत्रफल -
हमें यह नहीं पता की यह समकोण त्रिभुज है या नहीं अतः हम इसका क्षेत्रफल हिरो के सुत्र से ज्ञात करेंगे -
सबसे पहले अर्ध परिमाप s ज्ञात करेंगे = (8+10+6)/2 = 12
हिरो का सुत्र - √s(s-a)(s-b)(s-c)
= √12(12-6)(12-8)(12-10)
= √12(6)(4)(2)
= √576
A = 24
उदाहरण
एक समकोण त्रिभुज में कर्ण 5 सेमी. व लम्ब 3 सेमी हैं त्रिभुज का क्षेत्रफल होगा -
तिसरी भुजा निकालने के लिए
कर्ण2 = आधार2 + लम्ब2
आधार2 = कर्ण2 - लम्ब2
= 52 - 32
= 25-9
आधार2 = 16
आधार = 4
त्रिभुज का क्षेत्रफल - 1/2(3*4) = 6
उदाहरण
एक समबाहु त्रिभुज की एक भुजा 6 सेमी. है इसका क्षेत्रफल होगा -
समबाहु त्रिभुज की सभी भुजाएं समान होती है अतः क्षेत्रफल - √3/4*(भूजा)2
= √3/4*(6)2
= √3/4*36 = √39
उदाहरण
एक समकोण त्रिभुज में आधार व उंचाई में अनुपात 3:4 है। इसका क्षेत्रफल 96 सेमी है। इसका कर्ण होगा -
माना इसका आधार 3x व उंचाई 4x है तो क्षेत्रफल - 1//2*(3x*4x) = 96
= 12/2*x2 = 96
x2 = 96/6
x2 = 16
x = 4
आधार = 3*4 =12
उंचाई = 4*4 = 16
कर्ण2 = 122 + 16 2
कर्ण2 = 144 + 256
कर्ण2 = 400
कर्ण = 20
उदाहरण
एक समान्तर चतुर्भुज लम्बाई 4 सेमी. व चैड़ाई. 7 सेमी. है इसका क्षेत्रफल होगा -
समान्तर चतुभुर्ज का क्षेत्रफल = आधार*उंचाई
= 4*7 = 28
उदाहरण - एक समचतुर्भुज के विकिर्णों की लम्बाई क्र. 20 सेमी. व 10 सेमी. है इसका क्षेत्रफल -
समचतुर्भुज का क्षेत्रफल = 1/2 विकिर्णों का गुणनफल
विकिर्ण -20,10
क्षेत्रफल - 1/2(20*10) = 100
उदाहरण
एक समचतुर्भुज के विकर्णो की लम्बाई 24 सेमी. व 10 सेमी. है। इसका परिमाप होगा -
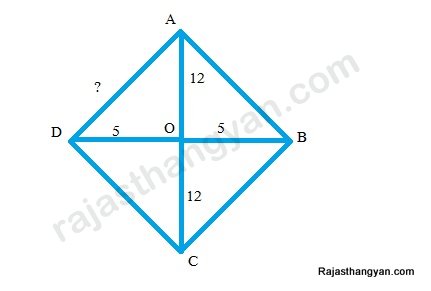
समचतुर्भुज के विकिर्ण एक दुसरे का समद्विविभाजित करते हैं अतः
त्रिभुज AOD
आधार -5 लम्ब - 12
कर्ण2 = 25 + 144
कर्ण2 = 169
कर्ण = 13
अतः समचतुर्भुज की एक भुजा 13 सेमी है तो परिमाप - 4* भुजा = 4*13 = 52
उदाहरण
एक वृत्त की परिधि 88 सेमी. तो त्रिज्या होगी -
परिधि = 2πr π=22/7
2πr = 88
2*22/7*r = 88
r= (88*7)/2*22
r=14
उदाहरण
एक पहिया 880 मी. दुरी तय करने में 10 चक्र लगाता है तो पहिये कि त्रिज्या क्या होगी -
एक चक्र पुरा करने में तय दुरी - 880/10 = 88 मी. यानि पहिये कि परिधि - 88 मी. है।
2πr = 88
r = 14
उदाहरण
बस के एक पहिये कि त्रिज्या 140 सेमी. इसे 60 किमी./घण्टा की गति के लिए प्रति मिनट कितने चक्र लगाने होंगे -
सबसे पहले बस की चाल मिटर/मिनट में बदलने पर = 60*1000/60 = 1000 मी./मिनट
पहिये कि परिधि = 2πr =2*22/7*140 = 88/10
एक चक्र में तय दुरी 88/10 मी. तो 1000 मी. दुरी तय करने में चक्रलगाने होंगे माना x
(88*x)/10 = 1000
x = (1000*10)/88 = 113.63 चक्र