रेखा गणित
हम अपने दैनिक जीवन में बहुत सारी आकृतियां देखते हैं और उनकी की लम्बाई चैड़ाई क्षेत्रफल आयतन आदि के बारे में जानना चाहते हैं। इन्हीं सवालों के हल के लिए हम रेखा गणित का अध्ययन करते हैं। रेखागणित आकृतियों और उनकी विशेषताओं के बारे में गणित है।
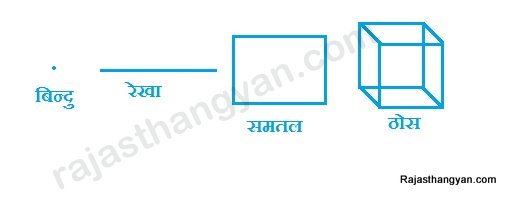
बिन्दु
बिन्दु का कोई आकार नहीं होता केवल स्थिति होती है।
रेखा
रेखा का किसी एक दिशा में विस्तार होता है।
समतल
समतल का विस्तार हमेशा दो दिशाओं में या अक्षों में होता है। इनकी केवल लम्बाई व चैड़ाई होती है। जैसे आयत,वर्ग,वृत्त आदि।
ठोस
वे सभी आकृतियों जिनका विस्तार तीनों अक्षों में होता है। अर्थात इसकी लम्बाई चैड़ाई व ऊंचाई भी होती है। जैसे गोला,शंकु आदि।
परिधि
किसी आकृति के किनारों के चारों तरफ की दुरी परिधि कहलाती है।

क्षेत्रफल
अगर साधारण भाषा में बात करें तो क्षेत्रफल किसी सतह का आकार है। या उस सतह द्वारा घेरा गया स्थान।

किसी भी समतल सतह का क्षेत्रफल ज्ञात करने के लिए हम उसकी लम्बाई ज्ञात करते हैं। तथा यदि लम्बाई और चैड़ाई एक समान हो तो लम्बाई को चैड़ाई से गुणा करते हैं। लम्बाई या चैड़ाई का एक समान होने का मतलब है की किसी आकृति की लम्बाई या चैड़ाई बीच से या किनारों पर से कम या ज्यादा न हो।
यदि हम यह जानना चाहें की क्षेत्रफल को ज्ञात करने के लिए लम्बाई को क्यों से गुना क्यों करते हैं तो एक उदाहरण लेते हैं इसमें एक आयत लेते हैं जिसकी लम्बाई 4 सेमी. है तथा चैड़ाई 3 सेमी. हैं अब इसका क्षेत्रफल ज्ञात करने के लिए हम इसके 1-1 सेमी. के टुकड़े करते हैं जो कि 12 होंगे। यानि लम्बाई की दिशा में 4 तथा चैड़ाई की दिशा में 3 अब सभी टुकड़ों को जोड़ते हैं तो क्षेत्रफल होगा 12 सेमी. जो की 4 और 3 का गुना हैं लम्बाई चैड़ाई में से एक को बढ़ा कर दुसरे को उतना ही कम कर दिया जाये तो क्षेत्रफल पर कोई प्रभाव नहीं पड़ेगा। यह निचे चित्र में दर्शाया गया है।
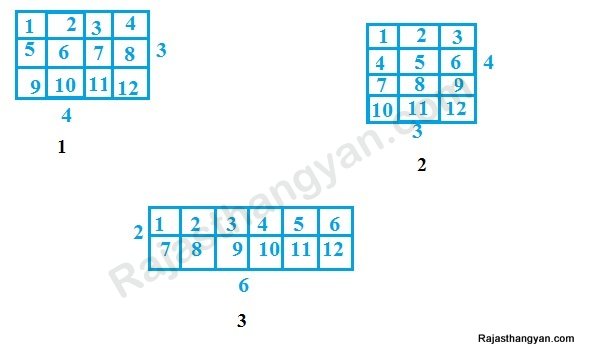
इस प्रकार हम कह सकते हैं कि किसी भी वस्तु जिसकी लम्बाई तथा चैड़ाई एक समान हैं चाहे वह आयत हो या वर्ग या वृत लम्बाई तथा चैड़ाई को गुना कर उसका क्षेत्रफल ज्ञात किया जा सकता है।
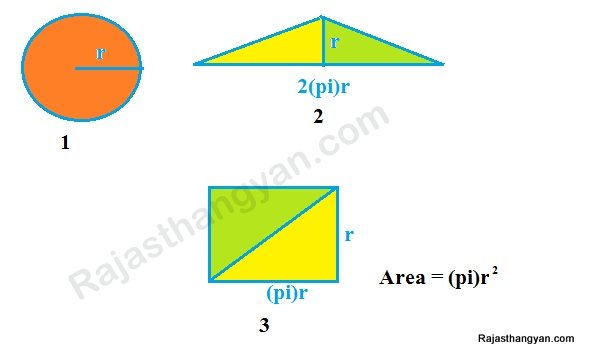
वृत का क्षेत्रफल ज्ञात करने के लिए हमें एक राशि पाई π (pi)की आवश्यकता होती हैं तो सबसे पहले जान लेते हैं पाई है क्या ?
पाई π - 22/7 या 3.14159 एक संख्या हैं। वास्तव में पाई का मान 22/7 नहीं होता है। क्योंकी 3.14159..... एक अपरिमेय संख्या हैं जिसे किसी भी परिमेय संख्या यानि p/q के रूप में नहीं दर्शाया जा सकता। पाई यह मान आया है। वृत के व्यास और परिधि में एक अनुपात पाया जाता है जिसका मान पाई या 3.14159.. होता है। यह अनुपात परिधि को व्यास से भाग देने पर आता है।
पाई दिवस 14 मार्च को मनाया जाता है। पाई का Symbol π है।
वृत का क्षेत्रफल भी लम्बाई गुना चैड़ाई से ज्ञात किया जा सकता है उदाहरण के लिए हम r त्रिज्या का एक वृत लेते हैं तथा इसे बिच से काट के चित्र के अनुसार फैला देते हैं जो कि दो त्रिभूजों के रूप में सामने आता है दोनों की लम्बाई 2πr जो कि वृत की परिधी हैं तथा ऊंचाई r जो की वृत की त्रिज्या हैं के रूप में दिखाई देता है अब दोनों त्रिभूजों को उलटा कर एक दुसरे के उपर रखने पर यह πr लम्बाई तथा r चैड़ाई का एक आयत बन जाता है जिसका क्षेत्रफल πr2 (लम्बाई*चैड़ाई)है। अतः वृत का क्षेत्रफल πr2 होता हैं